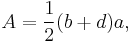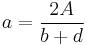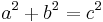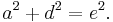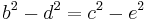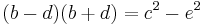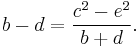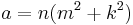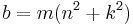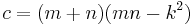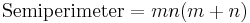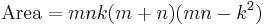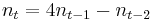Heronian triangle

In geometry, a Heronian triangle is a triangle whose sidelengths and area are all rational numbers. It is named after Hero of Alexandria. Any such rational triangle can be scaled up to a corresponding triangle with integer sides and area, and often the term Heronian triangle is used to refer to the latter.

Contents

Properties

Any triangle whose sidelengths are a Pythagorean triple is Heronian, as the sidelengths of such a triangle are integers, and its area (being a right-angled triangle) is just half of the product of the two sides at the right angle.

An example of a Heronian triangle which is not right-angled is the one with sidelengths 5, 5, and 6, whose area is 12. This triangle is obtained by joining two copies of the right-angled triangle with sides 3, 4, and 5 by the side of length 4. This approach works in general, as illustrated in the picture to the right. One takes a Pythagorean triple (a, b, c), with c being largest, then another one (a, d, e), with e being largest, constructs the triangles with these sidelengths, and joins them together by the side of length a, to obtain a triangle with integer sidelengths c, e, and b + d, with rational area

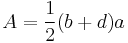A=\frac{1}{2}(b%2Bd)a (one half times the base times the height).

An interesting question to ask is whether all Heronian triangles can be obtained by joining together two right-angled triangles described in this procedure. The answer is no. If one takes the Heronian triangle with sidelengths 0.5, 0.5, and 0.6, which is just the triangle described above shrunk 10 times, it clearly cannot be decomposed into two triangles with integer sidelengths. Nor for example can a 5, 29, 30 triangle with area 72, since none of its altitudes are integers. However, if one allows for Pythagorean triples with rational entries, not necessarily integers, then the answer is affirmative,[1] because every altitude of a Heronian triangle is rational (since it equals twice the rational area divided by the rational base). Note that a triple with rational entries is just a scaled version of a triple with integer entries.

Theorem

Given a Heronian triangle, one can split it into two right-angled triangles, whose sidelengths form Pythagorean triples with rational entries.

Proof of the theorem

Consider again the illustration to the right, where this time it is known that c, e, b + d, and the triangle area A are rational. We can assume that the notation was chosen so that the sidelength b + d is the largest, as then the perpendicular onto this side from the opposite vertex falls inside this segment. To show that the triples (a, b, c) and (a, d, e) are Pythagorean, one must prove that a, b, and d are rational.

Since the triangle area is

A=\frac{1}{2}(b%2Bd)a,

one can solve for a to find

a=\frac{2A}{b%2Bd}

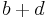which is rational, as both A and b%2Bd are rational. Left is to show that b and d are rational.

From the Pythagorean theorem applied to the two right-angled triangles, one has

a^2%2Bb^2=c^2\,

and

a^2%2Bd^2=e^2.\,

One can subtract these two, to find

b^2-d^2=c^2-e^2\,

or

(b-d)(b%2Bd)=c^2-e^2\,

or

b-d=\frac{c^2-e^2}{b%2Bd}.\,

The right-hand side is rational, because by assumption, c, e, and b + d are rational. Then, b − d is rational. This, together with b + d being rational implies by adding these up that b is rational, and then d must be rational too. Q.E.D.

Exact formula for Heronian triangles

All Heronian triangles can be generated [2] as multiples of:

a=n(m^{2}%2Bk^{2}) \,
b=m(n^{2}%2Bk^{2}) \,
c=(m%2Bn)(mn-k^{2}) \,
\text{Semiperimeter}=mn(m%2Bn) \,
\text{Area}=mnk(m%2Bn)(mn-k^{2}) \,

for integers m, n and k subject to the contraints:

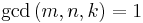
\gcd{(m,n,k)}=1
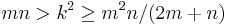
mn > k^2 \ge m^2n/(2m%2Bn)
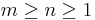m \ge n \ge 1.

See also Heronian triangles with one angle equal to twice another.

Examples

The list of fundamental integer Heronian triangles, sorted by area and, if this is the same, by perimeter, starts as in the following table. Fundamental means that the greatest common divisor of the three side lengths equals 1.

Area Perimeter length b+d length e length c
6 12 5 4 3
12 16 6 5 5
12 18 8 5 5
24 32 15 13 4
30 30 13 12 5
36 36 17 10 9
36 54 26 25 3
42 42 20 15 7
60 36 13 13 10
60 40 17 15 8
60 50 24 13 13
60 60 29 25 6
66 44 20 13 11
72 64 30 29 5
84 42 15 14 13
84 48 21 17 10
84 56 25 24 7
84 72 35 29 8
90 54 25 17 12
90 108 53 51 4
114 76 37 20 19
120 50 17 17 16
120 64 30 17 17
120 80 39 25 16
126 54 21 20 13
126 84 41 28 15
126 108 52 51 5
132 66 30 25 11
156 78 37 26 15
156 104 51 40 13
168 64 25 25 14
168 84 39 35 10
168 98 48 25 25
180 80 37 30 13
180 90 41 40 9
198 132 65 55 12
204 68 26 25 17
210 70 29 21 20
210 70 28 25 17
210 84 39 28 17
210 84 37 35 12
210 140 68 65 7
210 300 149 148 3
216 162 80 73 9
234 108 52 41 15
240 90 40 37 13
252 84 35 34 15
252 98 45 40 13
252 144 70 65 9
264 96 44 37 15
264 132 65 34 33
270 108 52 29 27
288 162 80 65 17
300 150 74 51 25
300 250 123 122 5
306 108 51 37 20
330 100 44 39 17
330 110 52 33 25
330 132 61 60 11
330 220 109 100 11
336 98 41 40 17
336 112 53 35 24
336 128 61 52 15
336 392 195 193 4
360 90 36 29 25
360 100 41 41 18
360 162 80 41 41
390 156 75 68 13
396 176 87 55 34
396 198 97 90 11
396 242 120 109 13

Almost-equilateral Heronian triangles

A Heronian triangle is a triangle with rational sides, area and inradius. Since the area of an equilateral triangle with rational sides is an irrational number, no equilateral triangle is Heronian. However, there is a unique sequence of Heronian triangles that are "almost equilateral" because the three sides, expressed as integers, are of the form n − 1, n, n + 1. The first few examples of these almost-equilateral triangles are set forth in the following table.

Side length Area Inradius
n − 1 n n + 1
3 4 5 6 1
13 14 15 84 4
51 52 53 1170 15
193 194 195 16296 56
723 724 725 226974 209
2701 2702 2703 3161340 780
10083 10084 10085 44031786 2911
37633 37634 37635 613283664 10864

Subsequent values of n can be found by multiplying the last known value by 4, then subtracting the next to the last one (52 = 4 × 14 − 4, 194 = 4 × 52 − 14, etc), as expressed in

n_t = 4n_{t-1} - n_{t-2} \,\!

where t denotes any row in the table.

This sequence (sequence A003500 in OEIS) can also be generated from the solutions to the Pell's equation x² − 3y² = 1, which can in turn be derived from the regular continued fraction expansion for √3.[3]

See also

External links

References

  1. ^ Sierpiński, Wacław, Pythagorean Triangles, Dover Publ., 2003 (orig. 1962).
  2. ^ Carmichael, R. D., 1914, "Diophantine Analysis", pp.11-13; in R. D. Carmichael, 1959, The Theory of Numbers and Diophantine Analysis, Dover.
  3. ^ William H. Richardson (2007), Super-Heronian Triangles.